Si bien el título esta escrito de forma llamativa a propósito, la teoría del optimal stopping también aplica a las relaciones amorosas, si lo vemos desde un punto de vista mas frio. A que me refiero con esto? Bien, supongamos que nosotros estamos en pareja durante un determinado tiempo, y sentimos que esa persona es el amor de nuestra vida, sin embargo es la primera vez que estamos en pareja con alguien y nunca antes habíamos estado enamorados/as, entonces no tenemos nada con que compararnos o medirnos, es decir como podemos estar en lo correcto si no conocemos a nadie mas?

Cómo encontrar el mejor lugar para estacionar?
Lo mismo aplica en muchos ordenes de la vida, por ejemplo supongamos que vamos a visitar a un amigo que vive en una zona de mucho tráfico y unas 3 cuadras antes de llegar a la casa vemos un lugar para estacionar el auto, ahí se presenta el dilema de si estacionar 3 cuadras antes y llegar caminando, o seguir en búsqueda de un lugar mejor sabiendo que no vamos a tener oportunidad de volver al lugar que encontramos y sin la certeza de que haya un lugar mejor mas adelante.

Como contratar al mejor candidato en un proceso de selección?
Otro ejemplo es cuando una empresa quiere contratar a alguien para un puesto de trabajo, suponiendo que tengamos N candidatos que nos enviaron un CV y queremos entrevistarlos para encontrar el indicado para el puesto y resulta que es un perfil tan difícil de encontrar que si no lo contratamos en el momento nunca vas podamos contratar a ese candidato, como podemos asegurarnos de que vamos a contratar al mejor? Si nos gusta el primero ya lo contratamos? Si nos gusta el quinto tenemos que detener la búsqueda y contratarlo sabiendo que si lo dejamos pasar no vuelve pero que si lo tomamos quizá el mejor esta mas adelante?
Optimal stopping
Todo esto tiene una respuesta matemática según el libro Algorithms to live by de Brian Christian, donde habla de como podemos aplicar algoritmos computacionales a nuestra vida diaria, en este caso el algoritmo llamado optimal stopping, muy util en informática, para cosas tales como calcular cuanto tiempo el procesador tiene que atender cada proceso, o cuanto tiempo asignar ciertos recursos a cada componente que lo requiera.
Entonces la respuesta a cuando dejar de buscar la mejor opción, viene dada de resolver el llamado problema de la secretaria, y no se trata de determinar que opción tomar, si no hasta donde seguir considerando nuevas opciones, y es en el 37% del total de disponibles para elegir.
En el problema de elegir la mejor secretaria, tenemos dos maneras de fallar, una es deteniéndonos antes y contratar sin haber descubierto una mejor, o deteniéndonos tarde y haber pasado la mejor opción, entonces tenemos que utilizar la regla del 37% para tener las mejores chances de no cometer este error (no es perfecto, solo reduce las chances de cometerlo).
Veamos un ejemplo:
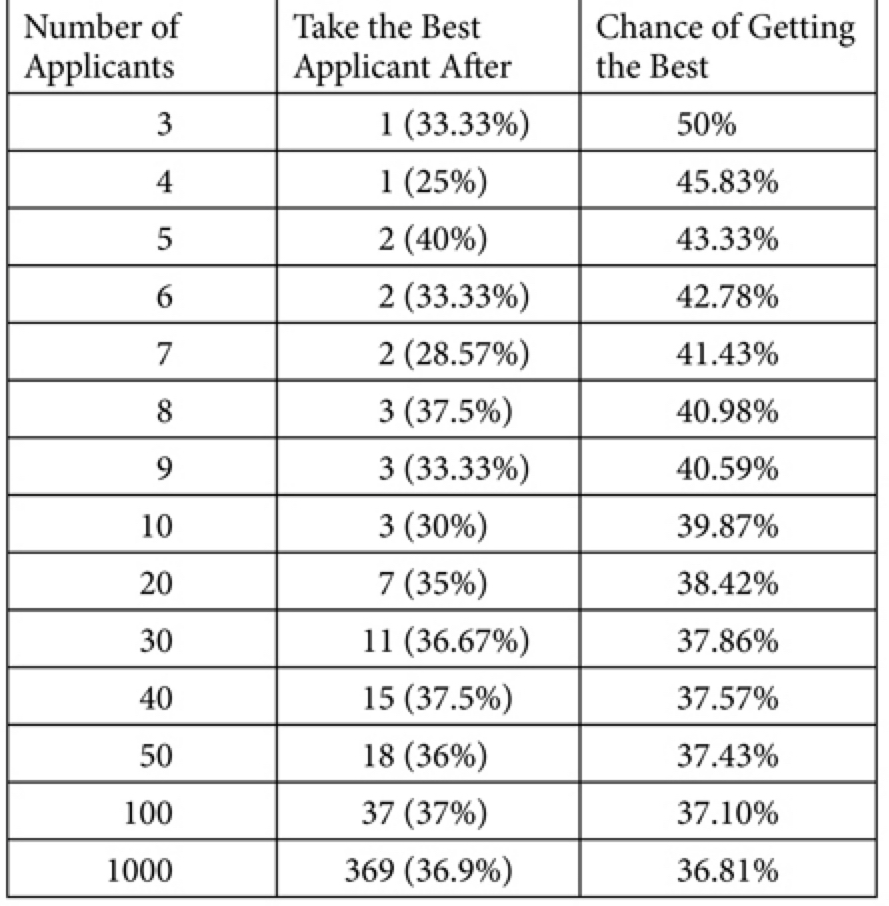
En este ejemplo vemos donde deberíamos parar de buscar dependiendo la cantidad de candidatos y cuales son las chances de lograr ese objetivo. Esta claro que no es un método perfecto ni nos garantiza obtener la mejor opción, solo nos indica el punto donde las chances de lograrlo son mayores.





